
In every educational process, the academic development of every student must be sought; the phases of academic development lead to memorization, then to deductive reasoning, then to developing the capacity for analysis and finally to develop the capacity for analytical abstraction, which is the door that leads us to academic conceptualization
Achieving academic conceptualization is something important and fundamental to develop a successful professional level of work; but, the most transcendental will be to reach the analytical conceptualization; which, is the one that brings us closer to the specific science; that is, to the origin of knowledge, to the root of the conceptual; in other words, to achieve synthesis over an analytical whole
When we develop analytical number, we conceptualize that the only mathematical analytical number that exists is one (1) and it will be a mathematical analytical whole that gives rise to an entire mathematical science of the arithmetic of integers; we remember again, an analytic number has no form, it is something completely intangible; the number form, as we know it (1) obeys our standard number system that we currently use; but in ancient times, both the Mayans, the Greeks, the Egyptians, also had that approach to the science of the arithmetic of integers and generated their own numerical system and represented the one (1) in different ways, but the analytical meaning will always be the same
The sciences, for their correct and functional understanding, must be classified according to their analytical conceptual origin; since, when we talk about a science in a very general way; it is very common, to be constantly updating it; for example, in general chemistry, the periodic table of natural elements is updated, as more different new natural elements are found, in the formation of our planet earth; but, when a specific science, we define it from its analytical conceptual origin; no longer, it is possible to make updates; since, the analytic origin encloses an absolute analytic whole; for this reason, it is not correct to speak of the mathematical sciences in general; if not, we should talk about each specific mathematical science, regarding its analytical conceptual origin
It is important in our lives to have an analytical conceptual understanding of how to quantify objects; that is, the mathematical science of the arithmetic of integers; since, in the real world, to have a working life development, it is necessary to quantify objects, quantify mathematical growths or decreases; but it is also necessary to have an understanding of analytical time; since it is very common to plan activities, structure a work agenda, where the organizational common is time; for this reason, having a deeper understanding of analytic time is essential
the conceptualization of analytical time gives rise to physical science
specifies the movement of bodies; we remember again, the analytic is something totally intangible; for this reason, time has no form, no one has seen time; like, that nobody has seen a mathematical analytical number; but, both analytic time and analytic number are fundamental
The conceptualization of analytical time gives rise to the specific physical science of the movement of bodies

To reach the origin or root of all specific science, we must arrive at the analytical abstraction of the analytically associated conceptualization, which gives rise to the specific science
The first thing that must be inferred is that time exists from the moment that everything around us is aging; if we realize, everything that exists in the universe follows an aging process; still, the new stars in formation, will also follow an aging process; for this reason, we perceive the light of many stars that perhaps at this time have ceased to exist
Time, we must understand it as something that has always existed, since the first thing that was formed in the universe exists, until that future time in which it finishes aging, the last thing that was formed in the universe
The human being, as part of a single existential process, will age and the time will come when he ceases to exist, as part of the universe; since, everything else continues to exist, following the aging process until they cease to exist
There is an analytical dimensional field, where the eternal exists; this analytical dimensional field is no longer located in the universe; that is, the 3D dimensional field as the universe is analytically known, 3D is that there are three dimensions and it is what our eyes can see; all analytical dimensional field, which is not 3D our sense of sight cannot see it
The eternal is something that is perpetual, something that will always exist; for this reason, in that analytical dimensional field of the eternal, time ceases to exist
Time is something analytical, we cannot see it, it is intangible, it has no form, but analytically we know that it exists and is related to our 3D world
For a long time in antiquity, civilizations had no understanding of time; at the time, if there were people with the necessary degree of development in analytical abstraction, they had the ability to analytically infer time, developing fairly accurate time measurement systems
Creating time measurement systems will be due to the human need to quantify moments; just as, the analytical number is born from the human need to quantify objects; analytical time is born from the human need to quantify moments; for that reason, ancient civilizations; having an understanding of time, they could already quantify moments related to the seasons and plan their harvests and other activities
Today, we use a standardized time measurement system; which, is based on a 24-hour day; furthermore, one hour is equivalent to 60 minutes and one minute is equivalent to 60 seconds; analytically we can infer it, that the only thing that exists is a second and then another second passes and so on without any purpose or continuing form; what our time measurement system tells us is that 60 seconds have elapsed and that is what we call a minute, then when 3,600 seconds have elapsed, we say that an hour has elapsed, until reaching the first 12 hours of the day; that is, what we call noon and corresponds to when the sun is at its highest and strongest in terms of heat; then we measure another 12 hours; and also, we can use the 24 hour format; which, after 12, follows a 13 that is equivalent to 1 pm, which is also expressed as the first hour past the meridian, until reaching the remaining 12 hours that end a day; that is, 86,400 seconds have elapsed and we continue with the first second of a new day and it will be a continuous measurement until reaching a year
The conceptualization of analytical time is born from the need to quantify specific moments of time

Starting from the human need to want to quantify moments, the study of analytical time arises; from very ancient civilizations, until the second was quantified as the only measure of time, with respect to the rotational movement of the planet earth on its own axis
It is important to infer analytically, that the second as time of standard measure; it is a specific space, in all the trajectory defined by time in general; but, regarding our planet earth and its rotation movement around its own axis; let us remember that all the planets in the universe do not necessarily take the same time to rotate around their own axis, some will be slower and others will be much faster to rotate around their own axis
Due to the above, we insist again on the importance that every process of academic development must be oriented towards the analytical; and thus, reach the degree of academic development that allows the student to delve into a specific academic study; but, following a deductive and functional reasoning
Whereas our time measurement system; where, the second as time measure is the fundamental base regarding the rotational movement of our planet earth; we can conclude that time itself cannot be assigned a standardized measure; since, it will be functional on our planet but not on other planets with life conditions very similar to our planet; but, they do not necessarily take the same time to rotate around their own axis; and even more, they do not necessarily take a year of ours, in going through their movement of translation with respect to their main star, according to their planetary system
Following the above, time continues to be something completely analytical, something that cannot be seen, completely intangible; but, we know that analytically it exists and is the fundamental basis for developing a specific measurement system like the one we currently use, where the second is the fundamental basis for measuring our time with respect to planet earth
The importance of any serious educational center is that it provides the student with all the necessary reasoning that allows him to develop that level of deductive reasoning and achieve a great capacity for analysis, which is the basis for great professional success in the future
It is important that everyone learns to measure time from an analog or digital clock; as well as, from any device that allows measuring time; but, if one of these people or several of these people, had the opportunity to attend an educational center and have reached the level of schooling where the physical sciences of time and movement are studied; must have the ability to interpret time as something completely analytical
Interpreting time from something completely analytical is the fundamental basis for having a great capacity in organizational management; when it comes into existence, an executive with a very high level of academic preparation and great corporate successes; one of his main work tools is the management and coordination of organizational time; which is an interpretation of analytic time
Regardless of the measurement system, time always remains in its analytical state

Starting from the conceptualization of analytical time, as a quantification of moments of life; that is, to be able to infer the second of time as an analytical whole of time, we can consider that the analytical second of time gives rise to the physical science of the movement of bodies
We are going to understand by a body, a defined quantity of mass that occupies a place in our physical space; for this reason, that body can be static; that is to say, without movement or it can be, in uniform movement; as well as, it can also have a variable movement
For example, trees are static physical bodies; since, a tree does not have the capacity to move or move from one point to another; however, animals such as dogs, cats can be considered as physical bodies that can undergo translational movement; like, that people; as well as, motor vehicles
We understand by translation movement, when a body moves from a specific initial point to another different point, as destination point; at the moment, that we have the second of time as a fundamental part of a system, which allows us to measure time; in addition, it is possible to measure the distance traveled; then, we can say that the body moved a specific amount of space covered; in addition, we can say that it took a specific amount of time to complete that journey
If we realize, when we consider movements of physical bodies, it will be possible to know the time it took to traverse the space used for translation; as well as, it will also be possible to measure that space covered; either in meters, in kilometers or some other way of measuring the distance traveled
At the end of having observed the physical body move from an initial point to an end point; as well as, knowing the number of meters he traveled; as well as the number of seconds of time it took to make that translation movement; we can affirm that the physical body moved S number of meters and did so in T number of seconds
At this time, we are able to infer something that is a complement to what was previously stated; that physical complement is what we call speed; then, at the moment that a physical body experiences a movement of translation, it had to do so with an implicit speed, the simplest type of movement of physical bodies, is when we consider that the physical body has a uniform speed; then it is possible to say that the physical body carried a uniform speed V = S / T
In other words, speed is implicit; something that is born, at the moment of having a movement of translation of a physical body; we can also call it, as a measure of speed; that is, how fast the physical body was going moving
Deductive reasoning tells us that speed exists when the body is in motion; since in general, a physical body starts from rest and ends up at rest or without movement, at the end of its journey; that is, that the speed V is something that exists only when the body is in motion; unlike, space S and time T which are always present, as part of something existential
the speed V is born as a consequence of being a physical body in motion, traveling through a space S in a specific time T

Whenever we receive academic learning, we must relate what we are learning to the real world; and above all, develop learning following an orderly deductive reasoning
When we learn the physical sciences of the movement of bodies; it is very common to start from theorems, from postulates; as well as, of a mathematical nomenclature; however, what is more important is to stay as close to the real world and use rational analytics to understand in an orderly rational way what we are learning
Continuing with the conceptualization of analytical time, it is important to observe that in the real world, the spaces S or the distances in meters that are considered for a specific physical situation, will always be something that we can measure; as well as, the time in seconds T for each physical situation considered, is something that we can also measure; instead, speed is something that is a relationship of two variables; that is, space S and time T; for example, when we walk we can see very clearly the distance in meters that we are covering; as well as, the time in seconds elapsed in our displacement, we can measure it in a clock; but, speed is something that we cannot measure so easily
We are going to consider that now we move using a motor vehicle, in this case if we can see on the speedometer at what speed we are moving; In general, speedometers indicate the speed in kilometers per hour; as well as, in miles per hour; it is very important, in all physical calculations we must do the measurement conversions; and so, stick to the standard units of measurement that are the meter for S and the second for T; for this reason, keep in mind that a kilometer is 1,000 meters, that a mile is 1,609 meters; as well as, an hour is 3,600 seconds
At the moment we walk, we begin to cover a distance and in parallel we are always subject to the time in seconds that is passing; for this reason, we can infer that when we walk we do so at a certain average speed; which, we can calculate knowing the number of meters we traveled and the time that elapsed, to make that journey; that is, that both S and T and V is something that is always linked to our lives
It is important to infer why V = S / T to reach that analytical inference; it is necessary to take the conceptualization associated with proportionality relationships; earlier, when we covered all the analytic number stuff, we talked about proportional growth trends; as well as non-proportional growth trends; in this case, we are going to consider the proportionality relationship between two variables
Suppose that T will be a constant, then what happens between V and S as proportionality relations; let’s imagine that we want to travel a distance S in a time T, then we will have a V as a result, but if we increase the space S to travel and we want to do it using the same time T, then we must necessarily increase the speed; that is, it is a direct proportional growth relationship; that is, S grows and V grows for this reason is that in the physical formula S appears as a numerator in the relation V = S / T
Now we are going to assume that S is a constant and we are going to observe what happens with the proportionality relationship between V and T if we realize that when traveling a distance S we do it with a speed V and we use a time T but at the moment that we want to travel the same distance S but in a shorter time; then, we definitely have to increase the speed V, that is, we have an inverse proportionality relationship; since, as T decreases, V increases as the relationship between the two variables is inverse; that is why, in the physical formula, T appears as a denominator in the physical formula
V = S / T
Understanding how physical formulas are born is something important in all academic development; and thus, we follow an orderly deductive rational reasoning, which will be part of the path that leads to academic and analytical conceptual development
V = S / T is born from the direct relationship of proportionalities between V and S as well as the inverse relationship of proportionalities between V and T

When the understanding of analytical time is had, it is possible to speak of speeds; that is, it is possible to calculate the average speed at which we move; since, it is possible to have the data of the space that we have traveled in meters; as well as, by means of a clock we can measure the time in seconds that it takes to travel that distance
To better understand the above, the first thing we learned to measure are the distances S since ancient times, but many forms of measurement were used until the meter was known as a measure; for this reason, any distance can be measured in meters; that is, that in real terms it will always be a known measure
When the human being had an understanding of analytical time and could get to know what a second of time lasts; then, every movement made; be it, a person walking, a person on a bicycle, a person in a car; It is possible to measure the time T in seconds that it takes to travel a specific distance or space S, that is, the time T is also a known real measure
The physical science of the movement of bodies, what it teaches us is to measure the speed of bodies in motion, using the physical formula V = S / T
the only thing we have to do is use the distance S in meters traveled as the numerator and use the time T in seconds that it takes to travel the distance S as the denominator when we do the division, we will obtain a ratio in meters/second, for example, suppose we go to cover 1000 meters and it takes us 100 seconds to cover them; so the average speed we experienced was V = S / T = 1000 m / 100 s = 10 m/s which tells us the answer is that the average speed was 10 meters per second; that is, we traveled 10 meters in each second and since the total number of seconds in the journey was 100 seconds; so, 100 x 10 = 1000
that is to say, that as in every second we traveled 10 meters; so, in 10 seconds we will travel 1000 meters
When we use a physical formula to make a specific calculation, we must always reason the result; to bring to our mind, the specific situation of the physical problem raised; and thus, every answer is reasoned in an orderly rational way
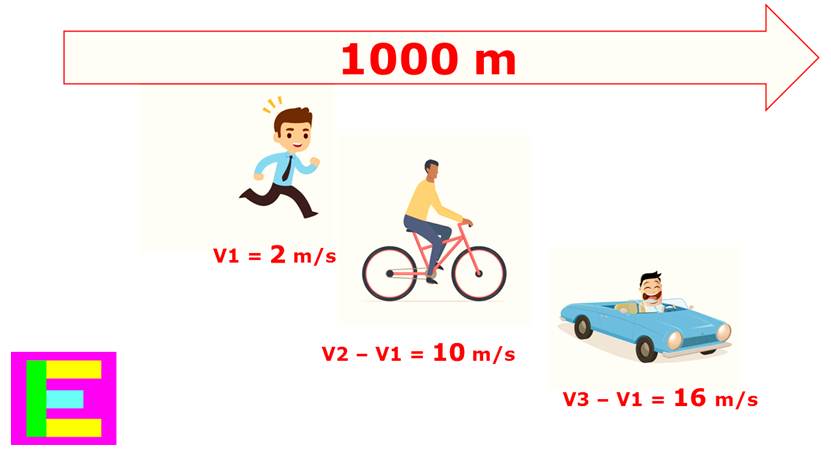
Continuing with the movement of bodies, it is interesting to mention that everything in the universe is in motion; for this reason, we must talk about relative physical movements; let’s suppose that in a 1000 meter path we have a person running with a speed V1 = 2 m/s then we have another person on a bicycle with a speed V2 = 12 m/s and we have another person in a car with a speed V3 = 18 m/s all on the same path of 1000 meters; the interesting thing will be that when the person who is running sees the person on a bicycle go by, the speed he will perceive will be V2 – V1, that is, 10 m/s, and when he sees the car go by, he will see it go by at a speed of V3 – V1 = 16 m/s and the person who rides a bicycle when seeing the car go by will see it go by at V3 – V2 = 6 m/s for this reason when two motorists go at the same speed, seeing each other in the moment they are parallel, the speed difference will be zero; that is, from either car it will appear that the other car is not moving
We see that the moon changes position; which, also corresponds to a relative perception; since the planet earth is rotating on its own axis at an average speed of 464 m/s and the moon is rotating around the planet earth at an average speed of 1020 m/s and we are located at a specific altitude and latitude; furthermore, the moon follows an elliptical path; which conditions the way we perceive its position
Everything in the universe is in motion; for this reason, all movements are relative to each other

To have an academic development, is to reach an orderly rational deductive reasoning, from what we learn academically and how we relate it to the real world
At the moment when the human being is aware of analytical time, the physical science of the movement of bodies is born; that is, to delve academically into the movement of bodies
At the moment that a body experiences a movement, we associate it with a distance S traveled; as well as, at a specific time T to cover the specific distance S, what we want to imply is that when a body experiences a movement; so, the body experiences a velocity V
From the above we can infer the following, a body can be at rest, that is, without any type of movement; as well as, it can be in movement; then, when a body is at rest it is not possible to associate a speed with it; at the moment, that the body moves; then experience a speed
Imagine a person who is sitting or lying down resting; at that moment, no speed can be associated with it; In other words, the speed does not exist when the person is at rest; now suppose, that the person moves; so, now it can be associated with a speed; that is, that speed exists at the moment that a body experiences a movement; since, it is going to move a distance S and it is going to do it in a time interval T
It is important to be aware that we are developing all the exemplifications at a basic level; since, the speed can have a specific direction and sense; as well as, the trajectories or the spaces traveled, are not necessarily linear; that is, they can be curved or have another type of relief; for this reason, it is that every physical academic problem must be reasoned, before applying the physical formulas
Continuing with the movement of the bodies, we can analyze the following, the space or trajectory S always physically exists in the real world; as well as, the time T that elapses when the body moves; for this reason, the speed V = S / T will always be present in that interval defined by the distance traveled S and the time elapsed T in traveling that distance; but now, we must consider what a scientist by his nature has the ability to infer analytically; and this is, that the speed can be increased; as well as, it can also be decreased; that is to say, that the body can experience a change of speed either ascending or descending; that is, increasing or decreasing
Due to the above, the physics of the movement of bodies is interested in studying that phenomenon that causes the speed to change; by analytically inferring, it is possible to say that there must be something external that makes the speed increase; In other words, when the speed increases it is because an acceleration is present; acceleration exists, when there is a change in speed; in other words, in the physics of the movement of bodies, when studying a body in motion; this, can have a constant speed; as well as, you may experience a change in speed; then the acceleration A exists whenever a body experiences a change in speed and so on; that is, as acceleration A is present, speed continues to vary; for this reason, when we drop a body from the highest; this is, subject to the gravitational law that incorporates an acceleration
A = 9.8 m/s^2, it is read meters over seconds squared; then, as the body falls, it increases its speed of fall
Acceleration A is present when there is a change in velocity from V1 to V2 and is given in meters per second squared; because the seconds are expressed squared, it indicates that the speed continues to increase; since, as time T elapses, a greater distance S is traveled per second

To achieve a high degree of academic development, it is necessary to always maintain the relationship between the real world and what we are learning; in the same way, it must be done in the different physical formulations; let us remember, that every physical formula relates the variables that leads us to the solution of a physical problem; but this will be, manifest in the real world; for this reason, physical formulations are made to operate under ideal conditions; since, in the real world everything is more complex; but, the approach between the physical formulation and the event in the real world, have a very close relationship
We have determined that the knowledge of analytical time leads us to the origin of the physical science of moving bodies; at the moment, that a body experiences a movement it is subject to travel a distance S in a time T for this reason, we infer in the knowledge of the speed, as a relationship between the space S in meters that we travel and the time T in seconds how long it took us to do it; at this time, we idealize speed as something constant; but in reality, we are going to observe that the speed is generally variable; then, a new physical understanding is born which is acceleration; we infer, the acceleration A is a differential of velocities in a defined interval of time; that is, A = ∆V / ∆T this is read as a delta V that is, a speed differential over a delta T that is, a time differential
At the moment that there is a change in speed, we analytically infer that for there to be a change in speed ∆V, the body must be subject to an acceleration We are going to idealize acceleration as something constant; then, a speed variation ∆V can be defined as a final speed minus an initial speed; time, as mentioned above, is something that we can measure
Acceleration is something that is always present in nature; for such reason, all physical science, starts from a simple observation; seeing, the fall of the bodies; in other words, every body that we drop, it is possible to observe that as it falls, its speed of fall increases; then, the academic understanding of the gravitational force is born; which, has a value of 9.8 m/s^2 which we can physically interpret as the constant acceleration experienced by a body in its fall
If we let a body fall freely, it will have an initial speed V1 = 0 since we only release it or let it fall; that is, it has no speed at start; then, at the end of its fall in a time interval ∆T that we can measure in seconds of time elapsed in its fall; we can, calculate the value of the final velocity V2 reached in that time course and subject to the constant acceleration of 9.8 m/s^2 for example, suppose we let a body fall freely and it takes 5 seconds to fall; then the final speed V2 reached is
V2 = A(T) + V1 as V1 is 0 then V2 = A(T) = A x T = 9.8 x 5 = 49 m/s now so that we have a clearer idea of how the speed of fall increases we are going to calculate the final speed V2 but for 6, 7, 8, and 9 seconds of fall; then, we get the following values of V2 58.8 m/s 68.6 m/s 78.4 m/s 88.2 m/s
The interesting thing about the previous exemplification; analytically speaking, it is that we can measure final speeds of fall and we see that they apparently follow a proportionality of increase; however, any constant acceleration causes the speed to increase during the time that the fall lasts; that is, the speed is growing and as it grows, it travels a greater number of meters per instant of time; for this reason, it is not possible to infer the space covered in a linear proportional way; position in the mind, how the distance traveled is covered at a speed that is increasing as a result of a constant acceleration, it will be something analytical inferential
The analytical inference of the way in which the speed increases when the body is subjected to a constant acceleration, makes us precise; that the space, that the body traverses increases as the time interval elapses; that is, all sorts of proportional linear relationships are lost for S

Developing deductive reasoning is essential in any process of academic development; but it will be essential, to achieve that ability to analytically infer a given situation
Analytical inference is a rational capacity that allows us to understand complex situations; taking as base, the analytical foundation; for this reason, we are going to exemplify how analytical inference is used in a specific physical situation
Let us consider the movement of free fall, to develop the following exemplification; suppose that, we release a body in free fall and we are going to calculate for each elapsed second, what is the value of the speed reached and how much space has it traveled in its fall
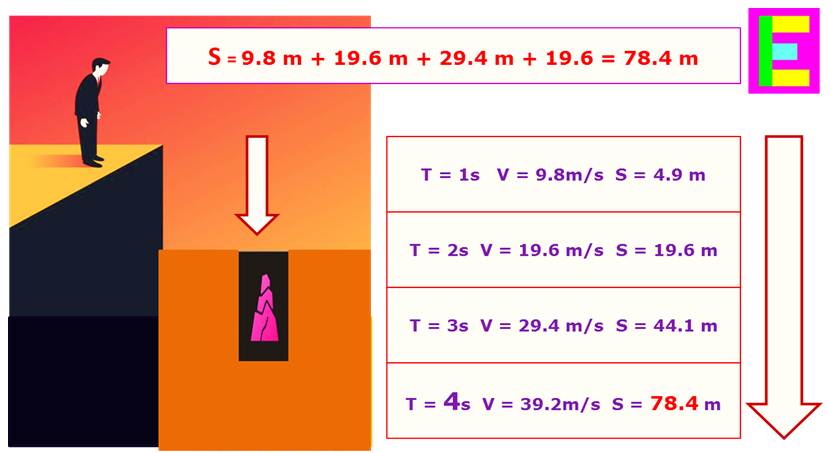
We are going to exemplify the first four seconds in his fall; according to the physical-mathematical formulation we can deduce an equation as a function of time, starting from the differential analysis; then, when the acceleration is constant, the kinematic equation is: X = Xo + VoT + 1/2AxT^2 in this physical-mathematical formulation, X is a variable that represents the space elapsed in free fall; as well as, X0 is the starting point; as well as, V represents the speed; where Vo is the initial velocity; as well as, A is the constant acceleration that is equal to 9.8m/s^2 and T is the time that elapses in the fall; expanding by the kinematic equation
T = 1 second S = 4.9 meters V = 9.8 m/s
T = 2 seconds S = 19.6 m V = 19.6 m/s
T = 3 seconds S = 44.1 meters V = 29.4 m/s
T = 4 seconds S = 78.4 meters V = 39.2 m/s
The above is a physical-mathematical way of solving the physical problem; now, let’s use analytic inference
The inferential analysis leads us to reason the physical problem in the following way; if we realize, in all free fall, the initial speed is always 0 and after the first second a speed of 9.8 m/s is reached, let us remember that A is a constant = 9.8 m/^2 as well as ∆T = 1 second considering that A = ∆V / ∆T then V = AT that is to say the final speed reached in the first second is the result of multiplying the acceleration A by the time T that is to say 9.8 x 1 = 9.8 m/s but we must consider that we start of a speed = 0 that is to say that the speed was increasing until reaching the value of 9.8 m/S at the end of the first second of fall time; furthermore, for each additional second we do the same calculation; only, that the time T is going to increase one by one; but, as the acceleration is always the same; then, analytically we have a proportional factor of 9.8
In addition, inferential analytics tells us that from second 1 to second 2 the body enters with a speed of 9.8 m/s and reaches 19.6 m/s, that is to say that in that second it necessarily had to cover 9.8 meters in its fall and a differential more than we do not know yet; Similarly, from second 2 to second 3, 19.6 meters of fall plus a differential are consumed; as well as, from second 3 to second 4, 29.4 meters of fall plus a differential are consumed; then,
9.8 m + 19.6 m + 29.4 m = 58.8 m now if we realize that in the speed reached 9.8 doubles to 19.6 m/s as well as 19.6 doubles to 39.2 m/s for this reason the proportional factor 9.8 is considered in two intervals of proportionalities; which gives us the remaining differential in meters of fall; that is, 9.8 x 2 = 19.6 m, then the total distance of fall in meters in the interval of four seconds will be 58.8 m + 19.6 m = 78.4 m the result coincides with the physical-mathematical methodology used
Inferential analytics is the ability to consider fundamental syntheses; as well as being able to reason, which determines the synthesis of the problem; that is, the fundamental factors that are present in all solution analytics

A physical formula must be interpreted as something academic conceptual and not as a recipe, where we substitute values and find unknowns; every process of academic development, must have as its ultimate goal in the student, to develop their capacity for analytical abstraction and thus have the ability to achieve academic analytical conceptualization; above all, in the different formulations, both physical and mathematical; as well as in other sciences
In the previous example, of calculating the spaces covered in the free fall of a body, the importance of reaching an analytical inference, to solve the physical problem, became clear; for this reason, we start from the basic conceptualization of S = VT, that is, every space covered is the result of its average speed multiplied by the time it took to cover it with that average speed; but, by applying analytic inference, we can also analytically conceptualize that the proportional space traveled is equal to the average proportional velocity times the proportional time elapsed in traveling the space
If we realize in the previous example of free fall, the proportionality of the speed is manifested in two proportional intervals, where the proportional factor is 9.8 m/s, let us remember that a body in free fall, the acceleration remains constant at 9.8 m/s ^2 for this reason the speed increases from 9.8 m/s to 19.6 m/s and after 19.6 m/s it grows to 39.2 m/s analytically there is a proportional factor acting in two proportionality intervals; in the same way, it happens with the fall time; since, from 0 to 4 seconds, it can be analytically inferred that there are two intervals of proportionality, which is from 0 to 2 seconds and the other proportional interval is from 2 seconds to 4 seconds; for this reason, that analytical space that cannot be appreciated so easily in free fall; since, the speed is increasing as a result of constant acceleration; then, that analytical space S was calculated starting from S = VT = (9.8m/s) x (2s) = 19.6 m to facilitate the understanding of the above, in free fall we can always determine the final speed in each second of fall; then, following the example, the falling body at the end of second 1 reaches a speed of 9.8 m/s and at the end of 2 seconds it reaches a speed of 19.6 m/s so from second 1 to second 2 it entered with a speed of 9.8 m/s and reached 19.6 m/s, then it is analytically inferred that he necessarily had to travel 9.8 m in T seconds if the speed were constant T = 1 second, but since the speed is variable; then, it travels one more differential in meters of fall that it is not possible to be able to perceive it so easily; for this reason is that it must be inferred analytically; as well as, it is analytically inferred that when it reaches the final speed of 39.2 m/s it is no longer possible for it to travel more space in meters; since, when reaching that final speed of 39.2 m/s, it also reached the ground; that is, it did not move anymore
Analytic inference is the basis for academic analytic conceptualization; for this reason, we can infer that the speed exists because the body begins to move; but, for a body to move, an external force is necessary to make the body move; that proportionally equitable distributed external force over the mass of a body is what we call acceleration A for this reason A = F / M, that is, acceleration is defined as a force in Newton Kg m/s^2 that is evenly distributed over a mass M measured in kilograms mass; to summarize, the physics of the movement of bodies V = S / T speed is defined by a body in motion that travels a distance S and takes a time T to travel it A = ∆V / ∆T acceleration is a variation of speeds in a time interval A = F / M acceleration is defined by a force acting on a mass
Acceleration manifests itself when a body undergoes a change in velocity: but, for acceleration to exist, there must be an external force acting, equally distributed over the mass of a body
