We invite you to refresh this page so that you can access the most updated 01 / 010

Using numbers is very common in our daily activities; now, in every mobile device we find numerical applications; that is, we learned to add, subtract, multiply, divide using numbers; but, at this moment it will be possible to clearly have in mind what is a number?
When someone is asked what is a number? in his mind he will position the shapes of the numbers we know; i.e. 1, 2, 3, 4, 5, 6, 7, 8, 9, but the question remains unanswered
In our basic school learning, we learned the form of numbers that we know and in an intuitive way, we assumed that a number can be any number form that we learned; in itself, what is happening is that we are confusing the analytic conceptualization of number with a number system; when we are in our basic school preparation, our mind has not developed enough to have the ability to reason; it becomes necessary, a whole process of academic preparation until reaching the ability to have a deductive reasoning and reach the ability of analytical abstraction, which will be the door that leads to analytical conceptualization
In ancient times, there were civilizations that had the ability to analytically infer what a number is and therefore created their own number systems; which, allowed them to be able to quantify material objects and others; if we realize, the number systems for each civilization are different; that is, they use various types of numerical representations; but, they express the same quantity; in other words, there may be many ways to represent a number system, but the analytical number conceptualization is unique
When we refer to analytical number, it is to reach the ability to analytically infer what a number is; analytically, a number has no form, it is something totally intangible, completely abstract; for this reason, it is in the category of analytical concepts
All academic conceptualization belongs to an analytical dimensional field; that is, just as there is a 3D dimensional field or a world in three dimensions; that is, everything we see, everything we can perceive, everything we can touch; also, it is possible to say that there are analytical dimensional fields; which, only the human mind can penetrate them, at the moment of having developed the capacity for analytical abstraction; it is surprising, as in ancient times, there were such brilliant minds that developed in a very convincing way the capacity for analytical conceptualization
The human mind has the ability to reach a high degree of development in analytical abstraction and has the ability to conceptualize the analytical

Achieving academic conceptualization should be the fundamental objective in any process of academic development; for this reason, there is basic academic training, secondary training and higher training; in which the sole objective is to develop the ability to conceptualize
To conceptualize is to reach analytical understanding; reaching analytical understanding is like reaching the seed that gave rise to a great tree; let’s imagine, we can see a large fruit tree, if we start to remove the earth around it, we will find the roots of the tree; at no time, we can find the seed that gave rise to it; in the same way, we learn to add, to subtract, to divide, to multiply; but, at no time, we have understanding of what an analytical number is, all arithmetic operations are like all the branches of that great fruit tree; but the seed is the conceptualization of analytical number; which, is the one that gave rise to all mathematical sciences
Just like wanting to see the seed of that great fruit tree, it is the analytical, that which is completely intangible, totally abstract; but, it will originate a whole set of related sciences; which will bring a great development to humanity
Analytical inference is born from the need to want to satisfy a human need; in ancient times, the Mayans as well as the Egyptians and the Greeks needed to quantify what they had, to know how much more they had, how much less they had, how to distribute what they had in equal parts; but, they did not have any numerical system that would allow them to be able to quantify numerically in an exact way; at the moment, of experimenting with different types of numerical systems, is when what an analytical number is inferred analytically; since, what they are looking for is the 1 (one) or the numerical analytical origin
When there is someone with the ability to have developed analytical abstraction, it is possible to determine that the only number that exists is 1 and 0 is the absence of any number or the absence of having something; then, to have is 1 to have nothing is 0 to have more, it is an accumulation of some 1 + 1 + 1 …
The above leads us to what is conceptually an analytical number; that is to say, conceptually, an analytical number means having at least 1 element and not having anything, that is to say 0 if we realize it, the result of the analytical conceptualization is intangible; since, the analytical response of numerical conceptualization is « to have quantitatively » at no time have we found as a result of the analytical conceptualization, some type of numerical symbology; for this reason, a great variety of number systems existed and were functional, until reaching the decimal number system, which is the one we currently use
Developing the capacity for analytical abstraction, allows reaching analytical conceptualization, that is, reaching the origin of academic knowledge
Narrative Pause
The mathematical boy
In that picturesque place, lived a very exemplary family which had only one son; which was well known in that place; since, he was someone very special, endowed with an extraordinary understanding in the sciences; for this reason, he was known as the mathematical boy
While the other children had fun playing various games, the mathematical boy spent hours and hours playing with numbers, adding them, subtracting them, multiplying them, dividing them; in short, the numbers for him were like his friends
One day, the father of the mathematical boy who was the main breadwinner in the family, suffers from a strange illness; which completely undermines his health, to the point that he keeps him bedridden
The family of the mathematical boy had a neighbor who was very identified with them; who, seeing the distressing situation they were going through, decides to tell them that he is soon to travel to a slightly distant place, where he is going to do some work; for this reason, he proposes that they allow the mathematical boy to travel with him and to help him; that is, that he serves as his assistant and thus he manages to get hold of some economic resources, while the father of the mathematical boy manages to overcome his state of health
The parents of the mathematical boy thanked him greatly for his good deed and allowed him to help them in the work that he was about to do in that distant place
The mathematical boy and the neighbor left very early in the morning, taking with them the necessary provisions for the long journey; they had already advanced a great distance, when they find a merchant in a very lonely place; which, tells them that he belongs to that place where they are going, but a merchant partner with whom he was traveling, had taken advantage of the fact that he was sleeping during the night, and had left with everything they were carrying, including all the provisions; luckily, he had 6 gold coins 🪙🪙🪙🪙🪙🪙 with him; which, was the only thing he had to get back to his place of origin, which was the same place where the neighbor and the mathematical boy were going
The merchant proposed the following, from what I see we have 6 days left on the road and we must survive the three with the provisions we have, I do not have any provisions; then the neighbor said, I have 4 loaves, 🥐🥐🥐🥐then the mathematical boy said, I have 2 loaves; 🥐🥐 the merchant said, I am willing to give you 4 gold coins for your four loaves and to you, referring to the mathematical boy, I will give you 2 gold coins for your two loaves; so that we can share the six loaves and manage to survive the three
The proposal seems very sensible to me, said the neighbor and from now on, I give my four loaves to the mathematical boy so that he is the one who takes care of the provisions and distributes them as he considers to be the most correct way to do it; and so, we manage to survive the three
The mathematical boy, who was highly gifted in understanding analytical sciences, took the six loaves and placed them in a container that he was carrying; in such a way that the first loaves to be distributed would be the four loaves of the neighbor and finally the two loaves that were his would be consumed
Each day of the journey, the mathematical boy took a piece of bread out of the container and divided it into three pieces; and so, they all managed to survive that day of the journey
At the end of the fourth day of the journey, the merchant said, I have seen that today the four days of the journey are over and we have all managed to survive; therefore, I have decided to give the neighbor the 4 gold coins that he had promised for the four loaves that he had contributed
At the end of the sixth day the merchant said, if you realize today marks the sixth day of the journey and there in the distance, we can already see the place where we must arrive; for this reason, I have decided to give the mathematical boy the 2 gold coins that correspond to him for the two loaves that he contributed; since, we have all managed to survive and we have reached the destination
The mathematical boy who had remained quiet throughout the journey, worrying about maintaining the custody of the provisions and distributing them according to how he established it, decides to take the floor to the astonishment of the merchant and speaks as follows, my very illustrious and respected merchant, I it seems that it is not fair economically speaking the way your 6 gold coins have been distributed and I am going to explain to you why I affirm the above
The problem that had to be solved was a problem of survival; that is to say, the three of us had to survive; suppose, your merchant partner had also taken your six gold coins from you; in the same way, both I and my neighbor would have always shared our bread with you and always in the end we would all have survived; more however, at the moment you assign the economic value of giving 1 gold coin for each loaf; 🪙 = 🥐 then the problem passes to the field of economics, as an analytical science and for this reason it must be solved following the rules and analytical laws that govern said economic science
Because your coins are gold they have a real economic value; for this reason, if they can be used as an economic exchange good
Giving each loaf the equivalent of a gold coin is also correct with respect to economic analytical science; since, both the four loaves of the neighbor and the two loaves of mine, replied the mathematical boy; they are elaborated, with natural economic resources and with home craftsmanship corresponding to the same geographical area
However, there is a preponderant analytical factor that is the intangible factor of survival; which, depending on the circumstances, will be its value; by the way, how I distributed the loaves; the first breads that were consumed were those of the neighbor; for this reason, they have a lower economic value; since, when we reached the sixth day of the journey, there was only one loaf left and it belonged to me, replied the mathematical boy and at that moment you still had 2 gold coins and my neighbor had 4 gold coins that you had already paid him; I, on the other hand, did not have any gold coins; but I assure you, that for that last piece of bread, you would have been able to blindly give me your 2 gold coins that you had left and my blind neighbor would have given me his 4 gold coins, both for the desire to survive
But if I had acted that way, the mathematical boy replied, I would have left the analytical economic laws completely and it would no longer have been a sale of bread, but it would have been a real robbery
To understand more about the event regarding economics as an analytical science, I will illustrate the following, each loaf was divided into three pieces; for this reason, since there were 6 loaves, then we had 18 pieces in total, but since there were three of us; each one of us was going to consume 6 pieces; but at the moment, when the merchant decides on the fourth day to give the 4 gold coins to the neighbor, then the economic circumstances of the event change; since, in the last two days of the journey, the neighbor already has economic resources; for this reason, it would not have been fair for me to be selling you the bread, referring to the merchant, and at the same time giving it to my neighbor, when he already had enough financial resources to pay for the bread he was consuming
For all of the above, the fairest thing in strictly economic terms would be for the neighbor to pay 2 gold coins; since, in total we had 18 pieces of bread and in total there were 6 gold coins as an element of economic exchange; that is, each piece of bread corresponds to an economic value of 1/3; in other words, each gold coin covers or satisfies 3 pieces of bread; but, as it is not possible for us to divide or split a gold coin into three parts; so the last 2 pieces of bread had an economic value of 2 gold coins; that is, for each piece of bread consumed on the fifth and sixth days of the journey, the merchant paid 1 gold coin for each piece of bread; for that reason, it is also fair that the neighbor pays his 2 gold coins; since, he also consumed two pieces of my breads, the mathematical boy finished
The merchant was speechless, having listened to all the illustrious economic explanation given by a little child, while the neighbor who already knew the mathematical child’s analytical skills, simply proceeded to give him the 2 gold coins without any objection and without mentioning any words
In the rest of the way, the neighbor took the opportunity to tell the merchant more about the mathematical boy’s analytical skills; since, the merchant was still very puzzled to have met a child with that level of understanding of science
Upon reaching the place where they were going, the merchant without hesitation told them, I want you to be my guests for the duration of your stay in this place, I also want the mathematical boy to help me count all my riches; as well as, he helps me organize all my goods, I will reward him in the best way
And so it was, both the neighbor and the mathematical boy had the opportunity to do various jobs and managed to return to their community of origin with enough earnings, which greatly helped the development of their community
The mathematician boy with the profits obtained, was able to give his father all the necessary attention, until he saw him fully restored, in addition his fame spread in such a way that they came from all places to make inquiries, bringing him many gifts; with which from then on, they lived with many economic comfortse


When we learn mathematics, the focus is on the operability of numbers; but, we stay completely away from mathematical analytical conceptualization
Numerical operability is important; but it is even more so, being able to reach the mathematical analytical conceptualization
To arrive at the mathematical analytical conceptualization is to arrive at the origin; that is, the mathematical analytical root, where an entire mathematical science is based
It is very common to say the science of mathematics as a whole; but, the correct thing is to refer to mathematics as a set of mathematical sciences; since, each mathematical science must have an origin or mathematical analytical root; that is, the analytical conceptualization that gave rise to that specific mathematical science
For an academic study to reach the category of science, it must be based on an analytical conceptualization
At the moment of arriving at the conceptualization of the mathematical analytical number, the mathematical science of the arithmetic of integers is born; we believe that this mathematical science is essential for anyone who wants to develop professionally, regardless of the field of work application; since, in all professional activity, we are going to be related to quantifications; that is, we need to know how much more I have, how much less I have, plan growth, etc.
The conceptualization of the analytical number leads us to the fact that the only number that exists is 1 and then what we have is an accumulated number of 1 depending on the specific quantity that we are considering; for example, 4 = 1 + 1 + 1 + 1 and so on, until reaching very large numbers; our numerical system is composed of nine different numerical forms 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0, its function is to simplify what is accumulated from 1, for this reason a very large number such as is 985 it would be very cumbersome to represent it as a cumulative of 1 but conceptually it is still a cumulative of 1
The 1 represents a whole, the science of mathematics of integers is the closest to our real world; that is, we count the things we have; for example, if we have oranges we are not going to be saying that I have five and a half oranges; our real life is related to integers; that is, either I have 5 oranges or I have 6 oranges; therefore, addition and multiplication are measures of growth; while subtraction and division are measures of decrease and among measures of accelerated growth, we have exponentiation; at no time, we must depart from the analytical conceptualization; the 1 is a mathematical whole, beyond 1 there are no more analytical conceptual numbers, when we segment the 1, that is, 1/n, the mathematical science of fractional numbers is born
The 1 as a mathematical whole originates the arithmetic science of integers


Achieving academic development is to leave the numerical operation and move towards orderly deductive reasoning
We have learned to add and we have learned to multiply; but, we have not been able to develop inferential deductive reasoning; which, allows us to infer that both addition and multiplication are growth operations; let’s consider the analytical conceptual, what we have is 1 or an accumulated of 1 in the case that we have more than 1 it is the moment that we have a growth, this can be proportional or non-proportional
When we add, what we have is a non-proportional growth; since, if we have 1 we can add any number; for example 1 + 5 we can also add 1 + 8 so I can add any number; for this reason, it is a non-proportional growth
In the case of multiplication it is a growth in proportions; since, if we multiply 3 x 4 = 12 what it means is that we have 3 and then we are going to have a growth in proportions of 3 four times; that is, 3 + 3 + 3 + 3 = 12 no matter what number we multiply it by 3, the growth will always be in proportions
When we manage to see addition as non-proportional growth and multiplication as growth in proportions; it will be, when we begin to have a deductive reasoning of what is actually happening; therefore, we are inferring the analytic conceptualization of the operations
Subtraction is a non-proportional decrease; since, like addition, I can subtract any number; for example, I have a total of 16. I am going to subtract 10 from it, so 16 – 10 = 6 the result is something specific and it is not possible to relate proportionalities; in the case of the division it is a decrease but the product of a proportional distribution; suppose that the 16 that I have, I am going to distribute among 8, then 16 ÷ 8 = 2, there was a decrease from 16 to 2 as a result of having proportionally distributed what I had, and every division will follow the same process of proportional distribution
Conceptually, both subtraction and division lead us to a decrease with respect to what it had; in the case of subtraction, it is non-proportional and in the case of division there is proportionality in the agreed distribution or among how many I am going to distribute, the greater the number of people with whom I am going to distribute, the greater my decrease will be with respect to what had
It is important to understand growths conceptually; since, the sum is a specific non-proportional growth, while the multiplication is a growth in proportions superior to the sum; for example, I sell oranges and in one day I sell 4 but if they have confirmed that they are going to buy 4 oranges for 5 days in a row, then it will be a multiplication of 4 x 5 = 20, the growth is higher; but, if I manage to develop sales of oranges with exponential growth, this will be the most superlative; since, 4 ^ 5 = 1,024 oranges, that is, he had 4 oranges, the second day 16 were sold, then 64 third day, then 256 fourth day and then 684 fifth day of oranges sold, then 4 + 16 + 64 + 256 + 684 = 1024 = 4 ^ 5 the exponential is the most superlative growth
We must develop the ability to conceptualize analytical growths

Developing conceptual reasoning will be fundamental in any process of academic development
To conceptualize is to have an analytical understanding of academic knowledge, we learn to memorize and we learn to operate numerically arithmetic operations; but the most important thing will be, to reach the degree of analytical abstraction; which, allows us to conceptualize and be able to develop a deductive analytical reasoning
We quantify, because we want to know how much we have, we can have more; as well as, we can get to have less; then, having something, then having more or later having less, is all that can happen in the real world, regarding quantifying material objects; for this reason, the sum operation is born; which tells us, that we have more
The operation subtracts, it is born when we have a diminution of what we had had; that is, that the subtraction tells us that we have less; when we distribute what we have among several, in the end we have less; that is, that the division is born, when it indicates that we have made a proportional distribution
The natural events to be quantified, with respect to having more or having less, can follow two trends; the proportional trend is when the growth is in equal proportions and the non-proportional trend is when the growth or decrease is not proportional
The arithmetic operation of multiplication tells us that we have growth in equal proportions; for example, 4 x 3 = 12 = 4 + 4 + 4 = 12
growth is in proportions of 4
The arithmetic operation of division indicates a decrease as a result of a distribution in equal proportions; that is, that we have inferred in a subtraction in equal proportions; for example, 18 ÷ 6 = 3 we can interpret this as a subtraction in proportions of – 3 – 3 – 3 – 3 – 3 – 3 that is, I have 18 but I give the first 3 then I also give the second 3 and so on up to the fifth; in the event, that the person who is dealing keeps 3; otherwise, it would be left with 0 when considering a sixth different person to distribute; in other words, I am doing subtraction in proportions of 3
If we realize, addition and multiplication go hand in hand; since both, lead us to growth; meanwhile, subtraction and division lead us to a decrease or a decrease; either growth or decrease, can be proportional or non-proportional
In order to measure advanced or superlative growth, exponentiation is used; an exponential growth is to take a base and then raise it to an exponential trend depending on the exponent we are using; for example 3 ^ 4 where the base is 3 and the exponent is 4 is equal to 3 x 3 x 3 x 3 = 81 in other words, we are going to multiply the base as many times by itself as the exponent indicates, then the growth will be disproportional; since, it will grow from 3 to 9 then to 27 then to 81 according to the above, it can be synthesized in that both addition, multiplication and exponentiation are measures of growth; being, the exponential growth the most superlative
Analytically, at the moment of having something, I can have a growth or I can have a decrease; either proportional or non-proportional

In all academic development, what we must achieve is science; the only way to get to science is through analytical conceptualization
How many sciences have we studied, but to what degree of analytical conceptualization have we managed to reach; only by reaching the level of development in analytical abstraction will it be possible to approach science
As long as the necessary degree of analytical conceptualization is not developed, we definitely do not know the science
Science is the base, it is fundamental, it is where every student who has the necessary means to undertake this task should be oriented; it is very common to talk about someone studying academic specializations; it is not possible to speak of an academic specialization when the basic science or the science that gave rise to the academic specialization is not known; this origin science is only known when you have the necessary mastery over the analytical conceptualization that gave life to the origin science
What always exists is the analytical dimensional field, where all the academic analytical concepts that may exist are immersed; when that group of people exist generationally, who manage to penetrate that analytical dimensional field due to the analytical abstraction capacity achieved, it is when the analytical conceptualization is inferred, which gives life to a new specific science; which must be associated with a series of academic knowledge; which must reach the student pedagogically; and above all, with an orderly deductive reasoning, which allows the student to relate the conceptual analytical part, with the real world where we live
When we learn only the operational part of any science, we are condemning science itself to its inevitable extinction; since the only thing that keeps any science alive is the analytical conceptual part; furthermore, when there is a group of people who have mastery over the analytical conceptual part of any science, it is when new utilities and new ways of using that specific science are discovered for the benefit of all humanity
Due to the above, when we talk about the science of mathematics, it is a complete mistake to refer to said science as an absolute whole; since, in the science of mathematics, there is a great variety of specific mathematical sciences, which are supported by a specific analytical conceptualization; which, keeps that specific mathematical science alive; furthermore, not all analytical conceptualizations associated with mathematics in general have been discovered
To exemplify the above, the specific mathematical science of the arithmetic of integers, its conceptual origin is the analytical conceptualization of mathematical analytical number; which, it is inferred that the only analytical number that exists is 1 which is a mathematical analytical whole
It is important to mention that the 1, as we currently know it, is only a type of standard symbology, associated with a standard numerical system, since the analytical one has no form, it is completely intangible; in other words, no one has ever seen an analytic number and no one ever will; for this reason, the Mayans, the Egyptians, the Greeks in ancient times, used several different symbologies to symbolize the 1 but they referred to the same mathematical analytical conceptualization
The analytical conceptual is what gives life to the origin of a specific science

Memorizing is our first step in any academic process; for this reason, when we learn to divide mathematically, what we follow is a rote procedure; which, teaches us where the dividend is placed; as well as, where the divider is placed; as well as, the type of symbology that we must use; that is, we follow a manual procedure that must be written on paper; and thus, it can be reviewed by our school teachers
All academic development process is very similar as when a great athlete or a great sportsman is prepared; that is to say, that every outstanding athlete or sportsperson must have a great training discipline; as well as, develop great abilities and skills on the sports discipline in which he is subjected
Our brain must be developed, in order to reach these high levels of rational development, just like any outstanding athlete, you must develop those parts of your body that will lead you to sporting success; in the case of our brain, it must achieve great academic successes
Achieving great academic success is reaching high levels of analytical conceptual understanding and having the ability to be successfully applied in the real world; in other words, reach a high professional level; that is, a successful working life
Taking advantage of all our basic school preparation in the best way will be essential for our brain or our rational mental capacity to develop efficiently; for this reason, it is that in our first steps in mathematics, we must learn manual procedures, which in the end are replaced by high-tech electronic devices; which, in a matter of seconds, gives us the mathematical result of operations that, due to the manual method, require a great deal of time and operational accuracy to obtain the result
Everything by heart or memory mind capacity, the time will come when naturally we have forgotten it; that is to say, our human mind has a great capacity to memorize a large amount of data, but like everything natural human, sooner or later we forget some things; since, we are constantly processing new mental data; for example, if at this moment we want to solve a square root by the manual method, it is most likely that we have already forgotten the manual resolution procedure
Due to the above, it is very important to achieve the ability to develop an analytical conceptual understanding; which, it is much more difficult to be able to forget it; since, in our brain, the analytical conceptual is not memorized, what is conceptualized; which is something that always remains present in our daily lives
In the case of the arithmetic of integers, as a basic tool in all development of academic and professional work life, what we must develop is the rational deductive understanding, which allows us at all times of our lives, to be conceptually very clear, growth operations, decrease operations and above all, understand mathematical complements; and thus, to be able to verify the mathematical results
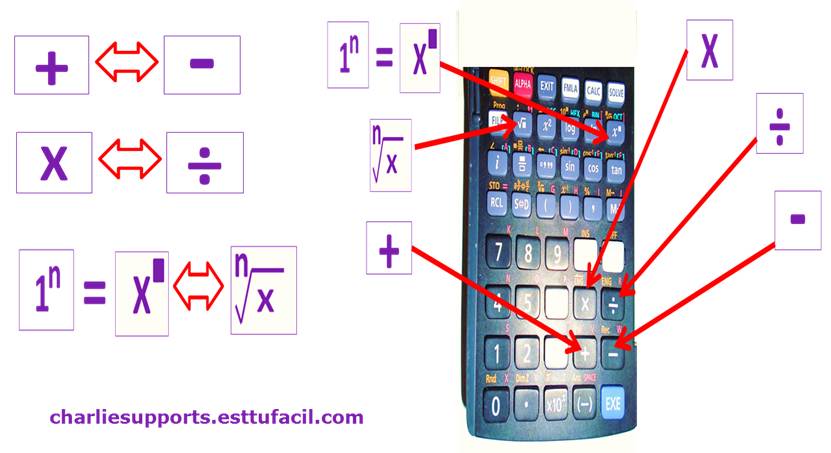
Addition is the mathematical complement of subtraction and vice versa; since, it is also possible to say, subtraction is the mathematical complement of addition; as well as, division is the mathematical complement of multiplication and vice versa; as well as, the exponentiation is the mathematical complement of the filing and vice versa
Mathematical analytical complements allow us to verify results

Understanding about mathematical complements is fundamental; since sooner or later in our professional life we will need to perform mathematical calculations and generally we will use some electronic device to do them, a mistake in the calculation can have very negative professional consequences
It is essential to be very clear about what a mathematical calculation complement means; since, it guarantees us that the final result of the mathematical operation is correct; for example, if we add 24 + 48 = 72, then as the subtraction is the mathematical complement of the addition, we proceed to carry out the verification mathematical calculation; then, 72 – 48 = 24 which corresponds to the first amount that we add, for this reason the calculation was correct
Division is the mathematical complement of multiplication; then, if we operate the multiplication 124 x 648 = 80352 then we use the division as verification operation; then, 80352 ÷ 648 = 124 which corresponds to the first quantity that we multiply, for this reason the calculation is correct
Radicalization is the mathematical complement of exponentiation; so if we operate the exponentiation 18^4 = 104976 then we use the filing as the verification operation; then, fourth root of 104976 = 18 which corresponds to the first quantity subject to exponentiation; for this reason, the calculation is correct
Today, with the high technology used in electronic mathematical calculation devices, it is very easy to perform very complex mathematical calculations and be able to check the result, let us remember that the mathematical operations of verification complements have the vice versa property; that is, if we subtract we use addition as a mathematical verification operation; for example, 174 – 83 = 91 when using addition as a mathematical verification operation; so, 91 + 83 = 174 which corresponds to the first quantity in the subtraction; for this reason, the calculation is correct
If we divide, we use multiplication as a mathematical verification operation; then,
855 ÷ 15 = 57 when using multiplication as a mathematical verification operation; then, 57 x 15 = 855 which corresponds to the first quantity of the division; that is, the calculation is correct
If we use radicalization, we must make use of exponentiation to verify the mathematical result; then 6th root of 262144 = 8 when using exponentiation as check complement math operation; we proceed to perform the exponentiation operation
8 ^ 6 = 262144 which corresponds to the quantity used in the sixth root; for this reason, the result is correct
When we are doing mathematical calculations at a professional level; it is not possible to make calculation errors; for this reason, it is important to have a great skill in the use of high-tech mathematical calculation devices; It is important to note that every electronic or digital device has no ability to reason at any time; that is, if the input of the data was incorrect, the result will be incorrect
The human being will always be the great coordinator; no matter how high technology we are using, only the human being has the ability to follow deductive reasoning; as well as, carry out all the necessary verification tasks so that his professional activity is successful
Imagine that before, calculation rules were used for complex mathematical operations; which, it was very difficult to carry out verification operations; today, there are very high-tech mathematical calculation devices; which, facilitate us, both the task of performing very complex calculations; as well as, the immediate verification of the result obtained; for this reason, the importance of reaching the mathematical academic conceptualization of the different mathematical operations
Verifying mathematical results is essential in any professional task

The entire science of integer arithmetic revolves around six mathematical academic conceptualizations; which are addition, subtraction, multiplication, division, exponentiation and radicalization
The six fundamental academic mathematical conceptualizations of integer arithmetic spring from the single mathematical analytic conceptualization of analytic number
Repeat again, the most important thing is to reach the origin; that is, to reach the analytical root that gives rise to the academic conceptualizations
When we only limit ourselves to learning operational methodologies, we do not achieve the necessary rational academic development that leads us to develop the degree of conceptual rational understanding; that is, the academic conceptualizations and especially the analytical conceptualization
An academic conceptualization is a rational deductive understanding, which allows us to understand the rational meaning of what we are operating mathematically; for this reason, we say that we conceptualize the sum as a non-proportional growth; whereas, we conceptualize multiplication as a proportional growth; as well as, the subtraction is a non-proportional decrease and the division is a decrease product of a proportional distribution; we also understand conceptually that exponentiation is a non-proportional superlative growth and radicalization is a superlative decrease, product of a decrease with an inverse exponential trend
It is also necessary to have a clear understanding of mathematical complements; and thus, to be able to verify the results obtained from mathematical operations; for this reason, subtraction is the mathematical complement of addition and vice versa; also, division is the mathematical complement of multiplication and vice versa; also, radicalization is the mathematical complement of exponentiation and vice versa
To all of the above, it is necessary to have a clear understanding of what proportionalities are; what we understand, when we refer to proportional growth or decrease; that is to say, that the growth or decrease will be in equal proportions; for example, 2 + 2 + 2 +2 … that is, it grows in equal proportions
When we refer to non-proportional growth or decrease, it is when there is no proportional trend in growth; for example, when there is exponential growth; for example, 2 ^ 4 = 16 so the growth is from 2 to 4 then from 4 to 8 at this point all proportionality is lost; since, to have maintained proportionality, the growth should be from 2 to 2, that is, from 2 to 4 then from 4 to 6, which does not occur in an exponential growth; for this reason, we call it a superlative growth
In our real world, regardless of professional work activity, we will always be immersed in the mathematical science of the arithmetic of integers; since, we need to add, subtract, multiply and other fundamental mathematical operations; in other words, everything that surrounds us in our real world, we quantify it; furthermore, everything real that exists is related to integers; but, the academic conceptual understanding places us at a higher level of quantitative understanding; which allows us to manage in a better way the patrimonial resources that we have achieved in life
Operating integers is fundamental, but understanding conceptually about mathematical operations will be something superior

Achieving academic conceptualization is what should be pursued in all academic development; thus, when the professional work level is reached, all our professional work activities will be coordinated by academic concepts rather than operational functions
Having a solid academic conceptual base opens up many possibilities to achieve great and sustainable professional success; to achieve sustainable professional results, it is necessary that they are based on academic conceptualizations
It is not possible to achieve academic conceptualizations if we have not achieved the analytical conceptualization; being very close to science implies having managed to achieve the analytical conceptualization that gave rise to science itself
When we conceptualize the mathematical analytical number, which is the basis of all arithmetic quantification, the arithmetic science of integers is born; which, gives rise to our current numerical system; as well as the mathematical operations of addition, subtraction, multiplication, division, exponentiation and radicalization
When we academically conceptualize the different mathematical operations; it will be when we get out of the rote operational part and begin to reason in a deductive way; for this reason we understand that addition and multiplication are growths and can follow a proportional trend or a non-proportional trend
Earlier it was said that the sum was non-proportional trend growth; since, we can add any number that generates a non-proportional growth trend; however, if we do a more exhaustive analysis, we can realize that the sum can have a growth with a non-proportional trend; but, it can also have a proportional growth; for example, we have 4 and we have an increase in 8, that is, 4 + 8 = 12, so now we have 12, but if we analyze the number 8, that is, the amount that we add; we can represent it as 2 + 2 + 2 + 2, this indicates that there was a growth in proportions of 2, that is, a growth with a proportional trend; in the same way, it will happen with the subtraction that can also generate a proportional decrease
When in our mind we position the proportional analysis; it will be when we begin to academically conceptualize the different mathematical operations
Academically conceptualizing direct proportionalities and inverse proportionalities will be fundamental in all mathematical academic development; since, all electronic device of mathematical calculation; no matter your level of technology, at no time will you be able to reason proportionalities; we repeat, only the human being has the capacity to reason; for this reason, if we are looking for technological development to be capable of reaching analytical conceptualizations; definitely that will never be possible
The analytical judgment of determining if a mathematical problem corresponds to a direct proportionality; that is, if factor one grows, then factor two also grows or if an inverse proportionality corresponds to it; that is, if factor one grows then factor two decreases, that analytical judgment only the human being is the one who is empowered to do it, above all technological advance regardless of the type of technology used
Only the human being has the ability to make analytical judgments above any technological advance, regardless of the type of technology used
